An Introduction to Statistical Learning

I’m continuing my journey through the classic textbook An Introduction to Statistical Learning. In this post, I’ll walk through my solutions for the Chapter 4 exercises, which cover the topic of Classification. This book is the work of Gareth M. James, Daniela Witten, Trevor Hastie, and Robert Tibshirani.
Learn
R
Author

Abdoulie Jallow

Published

November 14, 2024

Classification

Exercises

Conceptual

  1. Using a little bit of algebra, prove that (4.2) is equivalent to (4.3). In other words, the logistic function representation and logit representation for the logistic regression model are equivalent.

The logistic function is define as

\[ p(X) = \frac{e^{\beta_o + \beta_1X}}{1\;+ e^{\beta_o + \beta_1X}}\\ \tag{1}\]

Rearranging terms, \[p(X) = \frac{e^{(β₀ + β₁X)}} {1 + e^{(β₀ + β₁X)}}\] Let \(L = e^{(β₀ + β₁X)}\). Then \(p(X) = \frac{L}{1 + L}\).

\[\begin{gather*} p(X) \cdot{} (1 + L) = L\\ p(X) + p(X) \cdot{} L = L\\ p(X) = L - p(X) \cdot{} L\\ p(X) = L \cdot{} (1 - p(X))\\ \frac{p(X)}{(1 - p(X)} = L\\ \end{gather*}\]

Substituting \(L\) back gives the logit representation:

\[ \frac{p(X)}{1 - p(X)} = e^{\beta_o + \beta_1X} \tag{2}\]

  1. It was stated in the text that classifying an observation to the class for which (4.17) is largest is equivalent to classifying an observation to the class for which (4.18) is largest. Prove that this is the case. In other words, under the assumption that the observations in the kth class are drawn from a N(µk,σ2) distribution, the Bayes classifier assigns an observation to the class for which the discriminant function is maximized.

\[ p_k(x) = \frac{\pi_k\frac{1}{\sqrt{2\pi\sigma}} \cdot \exp(-\frac{1}{2\sigma^2}(x - \mu_k)^2)} {\sum_{l=1}^k \pi_l\frac{1}{\sqrt{2\pi\sigma}} \cdot \exp(-\frac{1}{2\sigma^2}(x - \mu_l)^2)} \tag{3}\]

The discriminant function is

\[ \delta_k(x) = x.\frac{\mu_k}{\sigma^2} - \frac{\mu_k^2}{2\sigma_2} + \log(\pi_k) \tag{4}\]

To show Equation 3 is equals to Equation 4, we first assume \(\sigma_1^2\;=\;...\;=\sigma_k^2\). Hence,

\[ p_k(x) = \frac{\pi_k \exp\left(-\frac{1}{2\sigma^2}(x - \mu_k)^2\right)} {\sum_{l=1}^k \pi_l \exp\left(-\frac{1}{2\sigma^2}(x - \mu_l)^2\right)} \]

Next, we take the \(\log(p_K(X))\) to linearized the function. \[ \log(p_k(x)) = \log(\frac{\pi_k \exp\left(-\frac{1}{2\sigma^2}(x - \mu_k)^2\right)}{\sum_{l=1}^k \pi_l \exp\left(-\frac{1}{2\sigma^2}(x - \mu_l)^2\right)}) \] Rearranging terms

\[ \log(p_k(x)) = \log(\pi_k) - \frac{1}{2\sigma^2}(x - \mu_k)^2 - \log\left(\sum_{l=1}^k \pi_l \exp\left(-\frac{1}{2\sigma^2}(x - \mu_l)^2\right)\right) \]

To maximize over \(k\), any term that’s independent of \(k\) is ignored

\[\begin{align} f &= \log(\pi_k) - \frac{1}{2\sigma^2} (x^2 - 2x\mu_k + \mu_k^2) \\ &= \log(\pi_k) - \frac{x^2}{2\sigma^2} + \frac{x\mu_k}{\sigma^2} - \frac{\mu_k^2}{2\sigma^2} \\ \end{align}\]

Since \(\frac{x^2}{2\sigma^2}\) is also independent of \(k\), it is ignored in order to maximize over \(k\)

\[ \log(\pi_k) + \frac{x\mu_k}{\sigma^2} - \frac{\mu_k^2}{2\sigma^2} \]

  1. This problem relates to the QDA model, in which the observations within each class are drawn from a normal distribution with a class-specific mean vector and a class specific covariance matrix. We consider the simple case where p = 1; i.e. there is only one feature.

Prove that in this case, the Bayes classifier is not linear. Argue that it is in fact quadratic.

To classify an observation, the Bayes classifier assigns it to the class \(k\) for which the posterior probability \(p_k(x)\) is largest. This is equivalent to assigning the observation to the class that maximizes the discriminant function, \(δ_k(x)\). For a one-dimensional QDA model, we do not assume the variances are equal across classes.

The discriminant function for class \(k\) is derived from the posterior probability: \[δ_k(x) = log(p_k(x)) = log(π_k \cdot{} f_k(x)) - log(C)\] where \(f_k(x)\) is the normal density \(N(μ_k, σ_k^2)\) and \(C\) is the denominator \(Σ P(Y=l)f_l(x)\), which doesn’t depend on \(k\). To maximize over \(k\), we can ignore \(C\).

Let’s expand the function: \[δ_k(x) ∝ log(π_k) + log(f_k(x))\] \[δ_k(x) = log(π_k) - log(√(2πσ_k^2)) - (\frac{1}{2σ_k^2}) \cdot{} (x - μ_k)^2\]

Expanding the squared term: \[δ_k(x) = log(π_k) - (\frac{1}{2})\;log\;(2πσ_k^2) - (\frac{1}{2σ_k^2}) \cdot{} (x^2 - 2xμ_k + μ_k^2)\]

Rearranging the terms to see the structure as a function of \(x\): \[δ_k(x) = - (\frac{1}{2σ_k^2})x^2 + (\frac{μ_k}{σ_k^2})x + [log(π_k) - (\frac{1}{2})log(2πσ_k^2) - (\frac{μ_k^2}{2σ_k^2})]\]

This discriminant function \(δ_k(x)\) is a quadratic function of \(x\). The coefficient of the \(x^2\) term is \(\frac{1}{2σ_k^2}\). Since QDA assumes that \(σ_k^2\) is different for each class \(k\), this quadratic term does not cancel out when comparing the discriminant functions of two different classes (i.e., when finding the decision boundary where \(δ_k(x) = δ_j(x))\).

Therefore, the resulting decision boundary is quadratic, and the Bayes classifier is not linear.

  1. When the number of features \(p\) is large, there tends to be a deterioration in the performance of KNN and other local approaches… This phenomenon is known as the curse of dimensionality… We will now investigate this curse.
  1. Suppose that we have a set of observations, each with measurements on \(p = 1\) feature, \(X\)… On average, what fraction of the available observations will we use to make the prediction?

Since \(X\) is uniformly distributed on \([0,1]\), its range is \(1\). The prediction for a test observation \(X=0.6\) uses training observations in the range \([0.55, 0.65]\). The length of this interval is \(0.65 - 0.55 = 0.1\). Because the data is uniform, the fraction of observations that fall into an interval is equal to the length of that interval. Therefore, on average, we will use \(10\%\) of the available observations.

  1. Now suppose that we have… \(p = 2\) features… On average, what fraction of the available observations will we use?

We are now in two dimensions, and we form a neighborhood by taking a \(10\%\) range for each feature. This creates a square (a 2-D hypercube) centered on the test point. The side length for this square is 0.1 for each dimension. Since the features are uniformly distributed on [0,1] x [0,1], the fraction of observations we use is the area of this square, which is \(0.1 \cdot{} 0.1 = 0.01\). So, on average, we will use only \(1%\) of the observations.

  1. Now suppose that we have… \(p = 100\) features… What fraction of the available observations will we use?

Following the pattern, for \(p=100\) dimensions, our neighborhood is a 100-dimensional hypercube where each side has length \(0.1\). The volume of this hypercube is \(0.1^{100}\). This is an infinitesimally small number, meaning we expect to use virtually zero fraction of the available observations.

  1. Using your answers… argue that a drawback of KNN when p is large is that there are very few training observations “near” any given test observation.

The answers to parts (a)-(c) show that the fraction of training data available in a local neighborhood of a fixed size (\(10\%\) of the range of each feature) decreases exponentially as the number of dimensions p increases \((0.1^p)\). For a large \(p\), this fraction is so small that the neighborhood is effectively empty. This means there are no “nearby” neighbors to average for a prediction, which undermines the entire principle of KNN and other local methods. This is the curse of dimensionality.

  1. Now suppose that we wish to make a prediction… by creating a p-dimensional hypercube… that contains, on average, \(10\%\) of the training observations. For \(p\) = 1, 2, and 100, what is the length of each side of the hypercube? Comment on your answer.

Let \(l\) be the side length of the p-dimensional hypercube. The volume is \(l^p\). We want this volume to be \(0.1\) (to capture \(10\%\) of the uniform data). So, we solve \(l^p = 0.1\) for \(l\), which gives \(l = (0.1)^{(1/p)}\).

  • For \(p = 1: l = (0.1)^{(1/1)} = 0.1\)
  • For \(p = 2: l = (0.1)^{(1/2)} ≈ 0.316\)
  • For \(p = 100: l = (0.1)^{(1/100)} ≈ 0.977\)
Note

As the dimension \(p\) increases, the side length \(l\) of the hypercube needed to capture just \(10\%\) of the data rapidly approaches \(1\). For \(p=100\), each side of the “local” neighborhood must span over \(97\%\) of the total range of its corresponding feature. This means the points within this hypercube are no longer truly “local” or “near” the test observation. The method loses its local character, and the predictions are based on points that are far away, which leads to poor performance.

  1. We now examine the differences between LDA and QDA.
  1. If the bayes decision boundary is linear, do we expect LDA or QDA to perform better on the training set? On the test set?

QDA been the more flexible model will perform better on the training set, but worse on the test set. On the test set, QDA will overfit the data because the true decision boundary is linear.

  1. If the Bayes decision boundary is non-linear, do we expect LDA or QDA to perform better on the training set? On the test set?

In this situation since the decision boundary is non-linear, QDA will perform better in both data sets. A linear model will underfit in this case.

  1. In general, as the sample size \(n\) increases, do we expect the test prediction accuracy of QDA relative to LDA to improve, decline, or be unchanged? Why?

As sample size increase, QDA will improve because there is more data to fit and the low bias will offset increase in variance.

  1. True or False: Even if the Bayes decision boundary for a given problem is linear, we will probably achieve a superior test error rate using QDA rather than LDA because QDA is flexible enough to model a linear decision boundary. Justify your answer.

False. In this case, QDA will overfit the data.

  1. Suppose we collect data for a group of students in a statistics class with variables \(X_1 =\) hours studied, \(X_2 =\) undergrad GPA, and \(Y =\) receive an A. We fit a logistic regression and produce estimated coefficient, \(\hat\beta_0 = -6\), \(\hat\beta_1 = 0.05\), \(\hat\beta_2 = 1\).

(a). Estimate the probability that a student who studies for 40h and has an undergrad GPA of 3.5 gets an A in the class.

\[ p(X) = \frac{e^{-6 + 0.05X_1 + X_2}}{1 + e^{-6 + 0.05X_1 + X_2}} \]

when \(X_1 = 40\) and \(X_2 = 3.5\), \(p(X) = 0.38\)

  1. How many hours would the student in part (a) need to study to have a 50% chance of getting an A in the class?

\[\begin{gather} \log\left(\frac{p(X)}{1-p(x)}\right) = -6 + 0.05X_1 + X_2 \\ \log\left(\frac{0.5}{1-0.5}\right) = -6 + 0.05X_1 + 3.5 \\ \end{gather}\]

Therefore, solving the equation \(0 = −6 + 0.05X_1 + 3.5\), \(X_1 = 50\) hours.

  1. Suppose that we wish to predict whether a given stock will issue a dividend this year (“Yes” or “No”) based on \(X\), last year’s percent profit. We examine a large number of companies and discover that the mean value of \(X\) for companies that issued a dividend was \(\bar{X} = 10\), while the mean for those that didn’t was \(\bar{X} = 0\). In addition, the variance of \(X\) for these two sets of companies was \(\hat{\sigma}^2 = 36\). Finally, 80% of companies issued dividends. Assuming that \(X\) follows a normal distribution, predict the probability that a company will issue a dividend this year given that its percentage profit was \(X = 4\) last year.

Hint: Recall that the density function for a normal random variable is \(f(x) =\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}\). You will need to use Bayes’ theorem.

Value of companies issuing a dividend (D) = \(D \sim \mathcal{N}(10, 36)\).

Value \(v\) for companies not issuing a dividend \((D^c)\) = \(D^c \sim \mathcal{N}(0, 36)\) and \(p(D) = 0.8\).

Bayes theorem:

\[\begin{align} P(D|X) &= \frac{P(D) \cdot{} P(X|D)}{P(D) \cdot{} P(X|D) + P(D^c) \cdot{} P(X|D^c)} \\ \end{align}\]

Substitute the Gaussian likelihoods into Bayes theorem

\[\begin{align} P(D|X) &= \frac{P(D) \cdot{} \frac{1}{\sqrt{2\pi\sigma^2}} e^{-(x-\mu_D)^2/2\sigma^2}} {P(D) \cdot{} \frac{1}{\sqrt{2\pi\sigma^2}} e^{-(x-\mu_D)^2/2\sigma^2} + P(D^c) \cdot{} \frac{1}{\sqrt{2\pi\sigma^2}} e^{-(x-\mu_{D^c})^2/2\sigma^2}} \\ \end{align}\]

Factor out \(\frac{1}{\sqrt{2\pi\sigma^2}}\) from the numerator and denominator, which cancels out:

\[\begin{align} P(D|X) &= \frac{P(D) \cdot{} e^{-(x-\mu_D)^2/2\sigma^2}} {P(D) \cdot{} e^{-(x-\mu_D)^2/2\sigma^2} + P(D^c) \cdot{} e^{-(x-\mu_{D^c})^2/2\sigma^2}} \\ \end{align}\]

Substitute the given probabilities and means:

\[\begin{align} P(D|X) &= \frac{0.8 \times e^{-(4-10)^2/(2 \times 36)}} {0.8 \times e^{-(4-10)^2/(2 \times 36)} + 0.2 \times e^{-(4-0)^2/(2 \times 36)}} \\ &= \frac{0.8 \cdot e^{-1/2}}{0.8 \cdot e^{-1/2} + 0.2 \cdot e^{-2/9}} \\ \end{align}\]

exp(-0.5) * 0.8 / (exp(-0.5) * 0.8 + exp(-2/9) * 0.2)
[1] 0.7518525
  1. Suppose that we take a data set, divide it into equally-sized training and test sets, and then try out two different classification procedures. First we use logistic regression and get an error rate of 20% on the training data and 30% on the test data. Next we use 1-nearest neighbors (i.e. \(K = 1\)) and get an average error rate (averaged over both test and training data sets) of 18%. Based on these results, which method should we prefer to use for classification of new observations? Why?

Logistic regression will perform better because it has a lower test error rate. For \(K = 1\), the training error rate is always zero because the closest point is always the training point itself, so the model will never make a mistake on the training set. Given that the average error rate for 1-NN is 18%, this implies a test error rate of 36%. Logistic regression, with a test error rate of 30%, is therefore the better choice.

  1. This problem has to do with odds.
  1. On average, what fraction of people with an odds of 0.37 of defaulting on their credit card payment will in fact default?

\[ \frac{p(x)}{1 - P(x)} = odd\\ \] \[\begin{equation} p(x) = \frac{odd}{1 + odd}\\ \end{equation}\]

\[\begin{equation} p(x) = \frac{0.37}{1 + 0.37} = 0.27 \end{equation}\]

  1. Suppose that an individual has a 16% chance of defaulting on her credit card payment. What are the odds that she will default?

\[\frac{0.16}{1 - 0.16} = 0.19\]

  1. In the setting with p = 1, (4.32) takes a simpler form…repeat the calculation in (4.32), and provide expressions for \(a_k\) and \(b_{kj}\) in terms of \(πk\), \(πK\), \(μk\), \(μK\), and \(σ2\).

The goal is to find the log-odds between class \(k\) and a baseline class \(K\) for an LDA model with \(p=1\). This is given by \(log(\frac{P(Y=k|X=x)}{P(Y=K|X=x)})\). This is equivalent to \(δ_k(x) - δ_K(x)\).

The discriminant function for LDA is: \[δ_k(x) = x \cdot{} (\frac{μ_k}{σ^2}) - (\frac{μ_k^2}{2σ^2}) + log(π_k)\]

The log-odds are: \[δ_k(x) - δ_K(x) = [x \cdot{} (\frac{μ_k}{σ^2}) - (\frac{μ_k^2}{2σ^2}) + log(π_k)] - [x \cdot{} (\frac{μ_K}{σ^2}) - (\frac{μ_K^2}{2σ^2}) + log(π_K)]\]

Now, group the terms that are constant and those that are coefficients of \(x\): \[= x \cdot{} (\frac{μ_k}{σ^2} - \frac{μ_K}{σ^2}) + [log(π_k) - log(π_K) - \frac{μ_k^2}{2σ^2} + \frac{μ_K^2}{2σ^2}]\]

This has the form \(a_k + b_{k1} \cdot{} x\). The coefficients are: \[a_k = log(\frac{π_k}{π_K}) - \frac{μ_k^2 - μ_K^2}{2σ^2}\] \[b_k1 = \frac{μ_k - μ_K}{σ^2}\] 11. Work out the detailed forms of \(a_k\), \(b_{kj}\), and \(b_{kjl}\) in (4.33). Your answer should involve \(πk\), \(μk\), \(Σk\). (Assuming (4.33) refers to the general quadratic form of the QDA discriminant function).

The QDA discriminant function is: \[δ_k(x) = -\frac{1}{2} \cdot{} log(det(Σ_k)) -\frac{1}{2} \cdot{} (x-μ_k)^T \cdot{} Σ_k^{-1} \cdot{} (x-μ_k) + log(π_k)\] Expanding the quadratic term \((x-μ_k)^T \cdot{} Σ_k^{-1} \cdot{} (x-μ_k)\): \[= x^TΣ_k^{-1}x - x^TΣ_k^{-1}μ_k - μ_k^TΣ_k^{-1}x + μ_k^TΣ_k^{-1}μ_k\] Since \(x^TΣ_k^{-1}μ_k\) is a scalar, it’s equal to its transpose \[μ_k^TΣ_k^{-1T}x = μ_k^TΣ_k^{-1}x\].

So the expression is \[x^TΣ_k^{-1}x - 2x^TΣ_k^{A-1}μ_k + μ_k^TΣ_k^{-1}μ_k\].

Substituting this back into \(δ_k(x)\): \[δ_k(x) = -\frac{1}{2} \cdot{} x^TΣ_k^{-1}x + x^TΣ_k^{-1}μ_k - \frac{1}{2} \cdot{} μ_k^TΣ_k^{-1}μ_k - \frac{1}{2} \cdot{} log(det(Σ_k)) + log(π_k)\] This is a quadratic function of \(x\). We can identify the constant, linear, and quadratic parts.

The constant term is \(a_k\): \[a_k = log(π_k) - \frac{1}{2} \cdot{} log(det(Σ_k)) - \frac{1}{2} \cdot{} μ_k^TΣ_k^{-1}μ_k\] The linear part is \(x^T(Σ_k^{-1}μ_k)\). The vector of coefficients for the linear terms is \(b_k = Σ_k^{-1}μ_k\). The coefficient for the j-th variable, \(x_j\), is: \(b_{kj} = (Σ_k^{-1}μ_k)_j\)

The quadratic part is \(-\frac{1}{2} \cdot{} x^TΣ_k^{-1}x\). The matrix of coefficients for the quadratic terms \(x_j \cdot{} x_l\) is \(-\frac{1}{2} \cdot{} Σ_k^{-1}\). The coefficient \(b_{kjl}\) is: \[b_{kjl} = (\frac{1}{2} \cdot Σ_k^{-1})_{jl}\]

  1. Suppose that you wish to classify an observation \(X \in \mathbb{R}\) into apples and oranges. You fit a logistic regression model and find that

\[ \hat{Pr}(Y=orange|X=x) = \frac{\exp(\hat\beta_0 + \hat\beta_1x)}{1 + \exp(\hat\beta_0 + \hat\beta_1x)} \]

Your friend fits a logistic regression model to the same data using the softmax formulation in (4.13), and finds that

\[ \hat{Pr}(Y=orange|X=x) = \frac{\exp(\hat\alpha_{orange0} + \hat\alpha_{orange1}x)} {\exp(\hat\alpha_{orange0} + \hat\alpha_{orange1}x) + \exp(\hat\alpha_{apple0} + \hat\alpha_{apple1}x)} \]

  1. What is the log odds of orange versus apple in your model?

The log odds (\(\frac{p(x)}{1 - P(x)}\)) in my model will be \(\hat\beta_0 + \hat\beta_1x\)

  1. What is the log odds of orange versus apple in your friend’s model?

Log odds of our friend model:

\[ (\hat\alpha_{orange0} - \hat\alpha_{apple0}) + (\hat\alpha_{orange1} - \hat\alpha_{apple1})x \]

  1. Suppose that in your model, \(\hat\beta_0 = 2\) and \(\hat\beta = −1\). What are the coefficient estimates in your friend’s model? Be as specific as possible.

The coefficient estimate in my friend’s model:

  • \(\hat\alpha_{orange0} -\hat\alpha_{apple0} = 2\)
  • \(\hat\alpha_{orange1} - \hat\alpha_{apple1} = -1\).
  1. Now suppose that you and your friend fit the same two models on a different data set. This time, your friend gets the coefficient estimates \(\hat\alpha_{orange0} = 1.2\), \(\hat\alpha_{orange1} = −2\), \(\hat\alpha_{apple0} = 3\), \(\hat\alpha_{apple1} = 0.6\). What are the coefficient estimates in your model?

The coefficients in my model would be \(\hat\beta_0 = 1.2 - 3 = -1.8\) and \(\hat\beta_1 = -2 - 0.6 = -2.6\)

  1. Finally, suppose you apply both models from (d) to a data set with 2,000 test observations. What fraction of the time do you expect the predicted class labels from your model to agree with those from your friend’s model? Explain your answer.

They should agree everytime (i.e, pridictions and log odd between any pair of classes will remain the same, regardless of coding). The cofficient will be different because of the choice of baseline.

Applied

  1. This question should be answered using the Weekly data set, which is part of the ISLR2 package. This data is similar in nature to the Smarket data from this chapter’s lab, except that it contains 1,089 weekly returns for 21 years, from the beginning of 1990 to the end of 2010.
  1. Produce some numerical and graphical summaries of the Weekly data. Do there appear to be any patterns?
library(ISLR2) # data sets
library(tidyverse)
library(psych) # for correlation plots
library(MASS) # for lda() and qda()
library(class) # for knn()
library(e1071) # for naiveBayes()
data("Weekly")
attach(Weekly)
str(Weekly)
'data.frame':   1089 obs. of  9 variables:
 $ Year     : num  1990 1990 1990 1990 1990 1990 1990 1990 1990 1990 ...
 $ Lag1     : num  0.816 -0.27 -2.576 3.514 0.712 ...
 $ Lag2     : num  1.572 0.816 -0.27 -2.576 3.514 ...
 $ Lag3     : num  -3.936 1.572 0.816 -0.27 -2.576 ...
 $ Lag4     : num  -0.229 -3.936 1.572 0.816 -0.27 ...
 $ Lag5     : num  -3.484 -0.229 -3.936 1.572 0.816 ...
 $ Volume   : num  0.155 0.149 0.16 0.162 0.154 ...
 $ Today    : num  -0.27 -2.576 3.514 0.712 1.178 ...
 $ Direction: Factor w/ 2 levels "Down","Up": 1 1 2 2 2 1 2 2 2 1 ...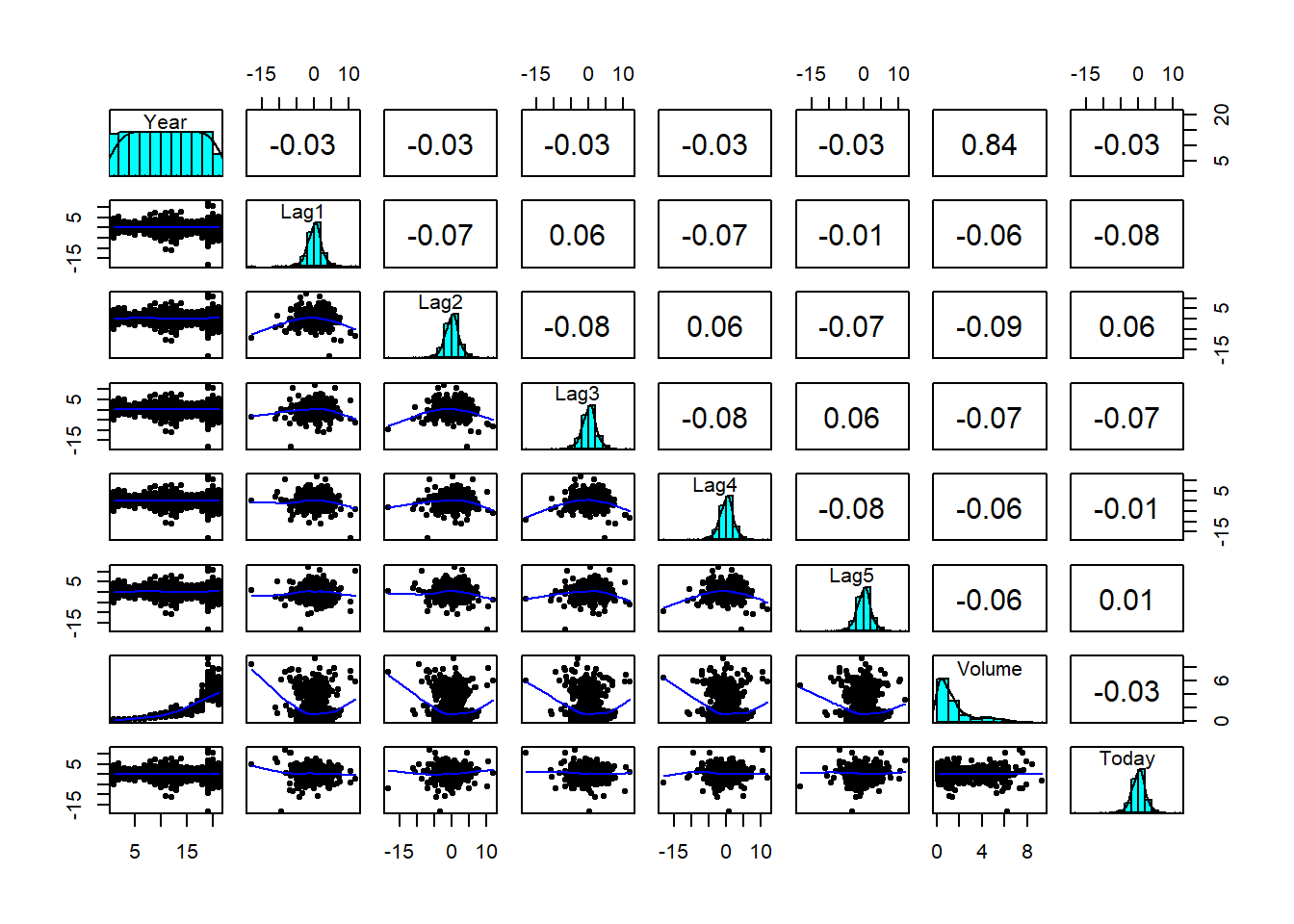
Weekly$Year <- as.factor(Weekly$Year)

pairs.panels(Weekly[1:8], cex.labels = 1, ellipses = FALSE)

# total number of times the market had a positive or negative return
table(Weekly$Direction)

Down   Up 
 484  605

There is a strong positive correlation between the volume of shares traded and the year. From 2005 to 2010, the volume of shares began increasing exponentially. Additionally, between 1990 and 2010, the market had a total of 605 positive returns and 484 negative returns, respectively.

  1. Use the full data set to perform a logistic regression with Direction as the response and the five lag variables plus Volume as predictors. Use the summary function to print the results. Do any of the predictors appear to be statistically significant? If so, which ones?
glm.fit <- glm(Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
               family = binomial)

summary(glm.fit)$coef
               Estimate Std. Error    z value    Pr(>|z|)
(Intercept)  0.26686414 0.08592961  3.1056134 0.001898848
Lag1        -0.04126894 0.02641026 -1.5626099 0.118144368
Lag2         0.05844168 0.02686499  2.1753839 0.029601361
Lag3        -0.01606114 0.02666299 -0.6023760 0.546923890
Lag4        -0.02779021 0.02646332 -1.0501409 0.293653342
Lag5        -0.01447206 0.02638478 -0.5485006 0.583348244
Volume      -0.02274153 0.03689812 -0.6163330 0.537674762

Among all the predictors, only Lag2 is statistically significant.

  1. Compute the confusion matrix and overall fraction of correct predictions. Explain what the confusion matrix is telling you about the types of mistakes made by logistic regression.
glm.prob <- predict(glm.fit, type = "response")
glm.pred <- ifelse(glm.prob > 0.5, "Up", "Down")

table(glm.pred, Direction)
        Direction
glm.pred Down  Up
    Down   54  48
    Up    430 557
# training error rate:
mean(glm.pred != Direction)
[1] 0.4389348

The 43.8% error rate is the training error. This is likely an optimistic estimate of how the model would perform on new, unseen data, as the model was evaluated on the same data it was trained on.

  1. Now fit the logistic regression model using a training data period from 1990 to 2008, with Lag2 as the only predictor. Compute the confusion matrix and the overall fraction of correct predictions for the held out data (that is, the data from 2009 and 2010).
train.data <- Weekly[Year < 2009, ]
test.data <- Weekly[Year > 2008, ]

glm.fit <- glm(Direction ~ Lag2, family = binomial,
               data = train.data)

summary(glm.fit)$coef
              Estimate Std. Error  z value   Pr(>|z|)
(Intercept) 0.20325743 0.06428036 3.162046 0.00156665
Lag2        0.05809527 0.02870446 2.023911 0.04297934
glm.prob <- predict(glm.fit, newdata = test.data, type = "response")
glm.pred <- ifelse(glm.prob > 0.5, "Up", "Down")

table(glm.pred, test.data$Direction)
        
glm.pred Down Up
    Down    9  5
    Up     34 56
mean(glm.pred == test.data$Direction)
[1] 0.625
# Test error rate
mean(glm.pred != test.data$Direction)
[1] 0.375

The model improved with Lag2 as the only the predictor. Test error rate is 37.5% which is better than random guessing.

  1. Repeat (d) using LDA.
# lda() is part of the MASS library
lda.fit <- lda(Direction ~ Lag2, data = train.data)

plot(lda.fit)

lda.pred <- predict(lda.fit, newdata = test.data)

names(lda.pred)
[1] "class"     "posterior" "x"        
table(lda.pred$class, test.data$Direction)
      
       Down Up
  Down    9  5
  Up     34 56
# test error rate
mean(lda.pred$class != test.data$Direction)
[1] 0.375
  1. Repeat (d) using QDA.
qda.fit <- qda(Direction ~ Lag2, data = train.data)

qda.pred <- predict(qda.fit, newdata = test.data)

table(qda.pred$class, test.data$Direction)
      
       Down Up
  Down    0  0
  Up     43 61
# test error rate
mean(qda.pred$class != test.data$Direction)
[1] 0.4134615
  1. Repeat (d) using KNN with \(K = 1\).
train <- (Year < 2009) 

train.Direction <- Weekly$Direction[train] # vector for the train class labels
test.Direction <- Weekly$Direction[!train] 

# knn() is part of the 'Class' library
set.seed(1)
knn.pred <- knn(Weekly[train, "Lag2", drop = FALSE],
                Weekly[!train, "Lag2", drop = FALSE], 
                train.Direction, k = 1)


table(knn.pred, test.Direction)
        test.Direction
knn.pred Down Up
    Down   21 30
    Up     22 31
# test error rate
mean(knn.pred != test.Direction)
[1] 0.5
  1. Repeat (d) using naive Bayes.
nb.fit <- naiveBayes(Direction ~ Lag2, data = train.data)

nb.pred <- predict(nb.fit, test.data)
table(nb.pred, test.data$Direction)
       
nb.pred Down Up
   Down    0  0
   Up     43 61
# test error rate
mean(nb.pred != test.data$Direction)
[1] 0.4134615
  1. Which of these methods appears to provide the best results on this data?

Logistic regression and linear discriminant analysis methods provide the best results on this data.

  1. Experiment with different combinations of predictors, including possible transformations and interactions, for each of the methods. Report the variables, method, and associated confusion matrix that appears to provide the best results on the held out data. Note that you should also experiment with values for \(K\) in the KNN classifier.
# Logistic Regression
glm.fit <- glm(Direction ~ Lag2 + Lag3 + Lag4,
               data = train.data,
               family = binomial)

glm.prob <- predict(glm.fit, newdata = test.data, type = "response")
glm.pred <- ifelse(glm.prob > 0.5, "Up", "Down")

table(glm.pred, test.data$Direction)
        
glm.pred Down Up
    Down    8  5
    Up     35 56
cat("Logistic error rate: ", mean(glm.pred != test.data$Direction))
Logistic error rate:  0.3846154
# Linear Discreminant analysis
lda.fit <- lda(Direction ~ Lag2 + Lag3 + Lag4, data = train.data)
lda.pred <- predict(lda.fit, newdata = test.data)

table(lda.pred$class, test.data$Direction)
      
       Down Up
  Down    8  5
  Up     35 56
cat("LDA error rate: ", mean(lda.pred$class != test.data$Direction))
LDA error rate:  0.3846154
# Naiv Bayes
nb.fit <- naiveBayes(Direction ~ Lag2 + Lag3 + Lag4, data = train.data)
nb.pred <- predict(nb.fit, test.data)

table(nb.pred, test.data$Direction)
       
nb.pred Down Up
   Down    7 10
   Up     36 51
cat("Naive Bayes error rate: ", mean(nb.pred != test.data$Direction))
Naive Bayes error rate:  0.4423077
# KNN

# Calculate error rates for each k
error_rates <- sapply(1:100, function(k) {
  train <- (Year < 2009)
  set.seed(1)
  
  knn.pred <- knn(Weekly[train, 2:4, drop = FALSE],
                  Weekly[!train, 2:4, drop = FALSE], 
                  Weekly$Direction[train], k = k)
  
  error_rate <- mean(knn.pred != test.Direction)
  return(error_rate)
})

# Find the k with the minimum error rate
min_error_rate <- min(error_rates)
best_k <- which.min(error_rates)
table(knn.pred, Weekly$Direction[!train])
        
knn.pred Down Up
    Down   21 30
    Up     22 31
# Print the result
cat("The best k is:", best_k, "with an error rate of:", min_error_rate, "\n")
The best k is: 26 with an error rate of: 0.3365385

After experimenting with several models and predictor combinations, the methods that provided the best results were logistic regression, LDA, and Naive Bayes using only Lag2 as a predictor. These models all achieved a test error rate of \(37.5\%\). The more complex models, including those with more predictors or the optimized KNN classifier, did not outperform this simpler baseline.